순열(permutation)이란 순서가 정해진 임의의 집합을 다른 순서로 섞는 연산을 말함
예를 들어 1, 2, 3이렇게 있을 때 1, 3, 2 이런식으로 다른 순서로 섞는 연산을 순열이라고 합니다.
그리고 n 개의 집합 중 n 개를 고르는 순열의 개수는 n!이라는 특징을 가지고 있으며 보통 중복을 허용하지 않는 기본조건이 있음
예를 들어 3개의 자연수(1, 2, 3)를 이용해 만들 수 있는 3자리 자연수는 몇개 일까요? 123, 132, 213, 231, 312, 321 이렇게 6개 입니다. 그렇다면 3개의 자연수(1, 2, 3)를 이용해 만들 수 있는 1자리 자연수는 몇개일까요? 3개입니다. 전자는 3개중 3개를 뽑는 것이라 3!이 되고 후자는 3개중 1개를 뽑는 것이라 3이 됩니다.
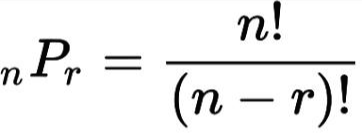
3개중 3개를 뽑는다면 3!/(3-3)!이 되고 3개중 1개를 뽑으면 3!/(3-1)!이 된다.
순열 생성 방법
1. next_permutation(오름차순)과 prev_permutation(내림차순)을 이용 -> next_permutation은 오름차순으로 순열을 만들 수 있을때 true, 아니면 false를 반환, prev_permutation는 내림차순으로 이와 반대
2. 재귀를 이용
1. next_permutation, prev_permutation 활용
#include <cstdio>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
void printV(const vector<int>& v)
{
for(int i = 0; i < v.size(); i++)
cout << v[i] << " ";
cout << "\n";
}
int main()
{
int a[3] = {1, 2, 3};
vector<int> v;
for(int i = 0;i < 3; i++) v.push_back(a[i]);
// 1, 2, 3부터 오름차순으로 뽑음
do
{
printV(v);
}
while(next_permutation(v.begin(), v.end()));
cout << "------------" << "\n";
v.clear();
for(int i = 2;i >= 0; i--) v.push_back(a[i]);
// 3, 2, 1부터 내림차순으로 뽑음
do
{
printV(v);
}
while(prev_permutation(v.begin(), v.end()));
return 0;
}
/*
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
------------
3 2 1
3 1 2
2 3 1
2 1 3
1 3 2
1 2 3
*/2. 재귀
#include <cstdio>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
int a[3] = { 1, 2, 3 };
vector<int> v;
void printV(const vector<int>& v)
{
for (int i = 0; i < v.size(); i++)
cout << v[i] << " ";
cout << "\n";
}
void makePermutation(int n, int r, int depth)
{
// 중간 결과 알아보기 위해(디버그용)
cout << n << " : " << r << " : " << depth << '\n';
if (r == depth)
{
printV(v);
return;
}
for (int i = depth; i < n; i++)
{
swap(v[i], v[depth]);
makePermutation(n, r, depth + 1);
// 원래 자리로 복귀(그래야 다음것을 바꿀 수 있음)
swap(v[i], v[depth]);
}
}
int main()
{
for (int i = 0; i < 3; i++) v.push_back(a[i]);
makePermutation(3, 3, 0);
return 0;
}
/*
3 : 3 : 0
3 : 3 : 1
3 : 3 : 2
3 : 3 : 3
1 2 3
3 : 3 : 2
3 : 3 : 3
1 3 2
3 : 3 : 1
3 : 3 : 2
3 : 3 : 3
2 1 3
3 : 3 : 2
3 : 3 : 3
2 3 1
3 : 3 : 1
3 : 3 : 2
3 : 3 : 3
3 2 1
3 : 3 : 2
3 : 3 : 3
3 1 2
*/

조금 복잡해 보이지만 간단하다. 필자는 분석이 꽤 걸렸지만, 알고보면 쉽다.
i와 depth 값이 다르면 위치를 바꾸는 구조다.
'C++ > 알고리즘' 카테고리의 다른 글
| <알고리즘> 모듈러 연산 (0) | 2022.04.21 |
|---|---|
| <알고리즘> 최대공약수/최소공배수 (0) | 2022.04.21 |
| <알고리즘> 조합(Combination) (0) | 2022.04.21 |
| <알고리즘> 구조체를 이용한 커스텀 정렬 (0) | 2022.04.19 |
| <알고리즘> Split (0) | 2022.04.12 |
