자료구조와 C++
자료 구조(data structure)는 효율적으로 데이터를 관리하고 수정, 삭제, 탐색, 저장할 수 있는 데이터 집합
#include <bits/stdc++.h> // --- (1)
using namespace std;// --- (2)
string a;// --- (3)
int main(){
cin >> a;// --- (4)
cout << a << "\n";// --- (5)
return 0; // - (6)
}
1. 헤더 파일입니다. STL 라이브러리를 import합니다. 이 중 bits/stdc++.h는 모든 표준
라이브러리가 포함된 헤더입니다.
2. std라는 네임스페이스를 사용한다는 뜻입니다. cin이나 cout 등을 사용할 때 원래는 std::cin처럼
네임스페이스를 달아서 호출해야 하는데, 이를 기본으로 설정한다는 뜻입니다. 참고로
네임스페이스는 같은 클래스 이름 구별, 모듈화에 쓰이는 이름을 말합니다.
3. 문자열을 선언했습니다. <타입> <변수명> 이렇게 선언합니다. string이라는 타입을 가진 a라는
변수를 정의했습니다. 예를 들어 string a = "큰돌"이라고 해봅시다. 이때 a를 lvalue라고 하며
큰돌을 rvalue라고 합니다. lvalue는 추후 다시 사용될 수 있는 변수이며, rvalue는 한 번 쓰고 다시
사용되지 않는 변수를 말합니다.
4. 입력입니다. 대표적으로 cin, scanf가 있습니다.
5. 출력입니다. 대표적으로 cout와 printf가 있습니다.
6. return 0입니다. 프로세스가 정상적으로 마무리됨을 뜻합니다.
빅오표기법, 시간복잡도와 공간복잡도
- 빅오 표기법 : ‘가장 영향을 많이 끼치는 높은 승수를 가진’ 항의 상수 인자를 빼고 나머지항을 빼서 나타낸 복잡도표기법
- 공간 복잡도 : 프로그램을 실행시켰을 때 필요로 하는 자원 공간의 양
- 시간 복잡도 : ‘문제를 해결하는 데 걸리는 시간과 입력의 함수 관계’

연결리스트와 배열의 차이
연결리스트
데이터를 감싼 노드를 포인터로 연결해서 공간적인 효율성을 극대화시킨 자료 구조입니다. 삽입과 삭제가 O(1)이 걸리며 탐색에는 O(n)이 걸림
#include <bits/stdc++.h>
using namespace std;
int main(){
list<int> a;
for(int i = 0; i < 10; i++)a.push_back(i);
for(int i = 0; i < 10; i++)a.push_front(i);
auto it = a.begin(); it++;
a.insert(it, 1000);
for(auto it : a) cout << it << " ";
cout << '\n';
a.pop_front();
a.pop_back();
for(auto it : a) cout << it << " ";
cout << '\n';
return 0;
}
/*
9 1000 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9
1000 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8
*/
배열
같은 타입의 변수들로 이루어져 있고, 크기가 정해져 있으며, 인접한 메모리위치에 있는 데이터를 모아놓은 집합입니다. 탐색에 O(1)이 되어 랜덤접근(random access)이 가능합니다. 삽입과 삭제에는 O(n)이 걸림.
#include <bits/stdc++.h>
using namespace std;
int a[10];
int main(){
for(int i = 0; i < 10; i++)a[i] = i;
for(auto it : a) cout << it << " ";
cout << '\n';
return 0;
}
/*
0 1 2 3 4 5 6 7 8 9
*/
따라서 데이터추가와 삭제를 많이 하는 것은 연결 리스트, 탐색을 많이 하는 것은 배열로 하는 것이 좋습니다. 배열은 인덱스에 해당하는 원소를 빠르게 접근해야 하거나 간단하게 데이터를 쌓고 싶을때 사용합니다.
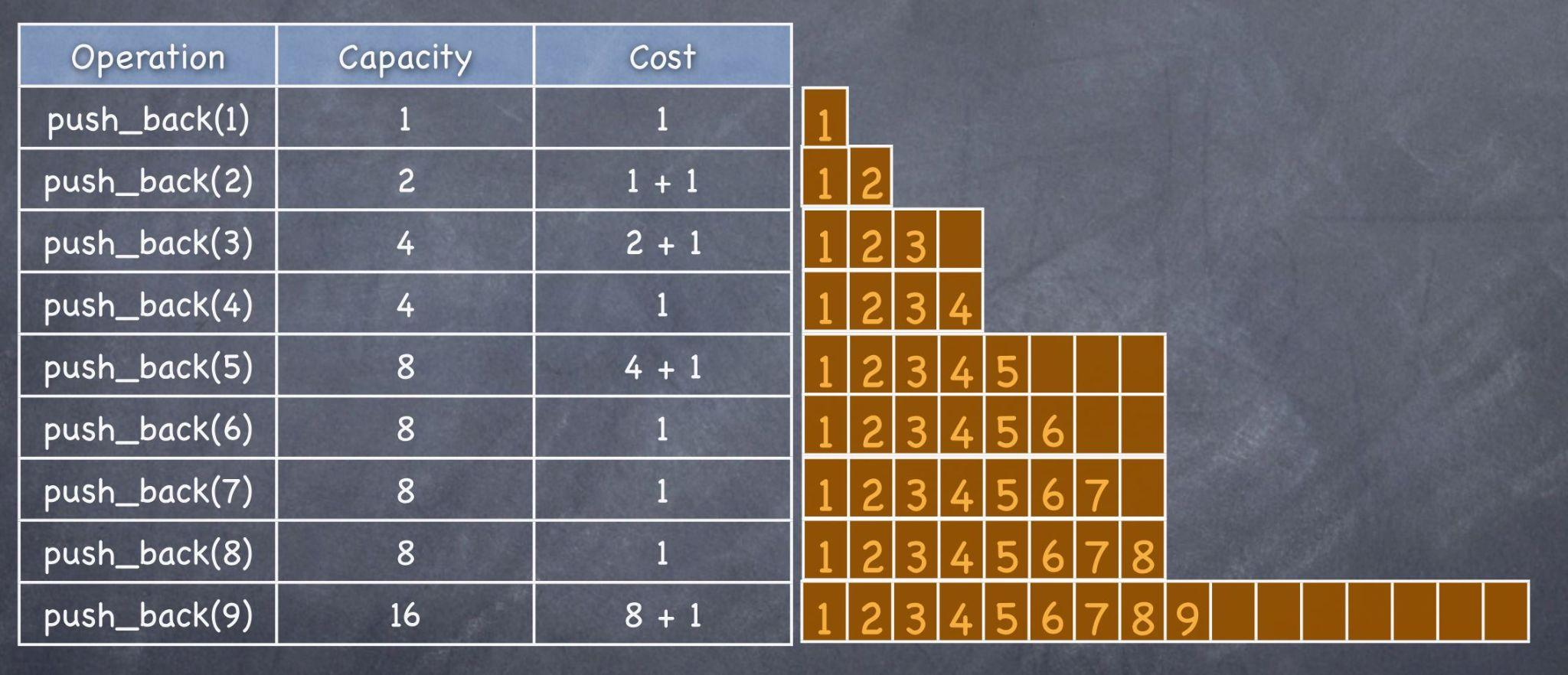
벡터와 push_back()의 시간복잡도가 O(1)인 이유
push_back()을 한다고 해서 매번 크기가 증가하는 것이 아니라 2의 제곱승+ 1마다 크기를 2배로 늘려짐.

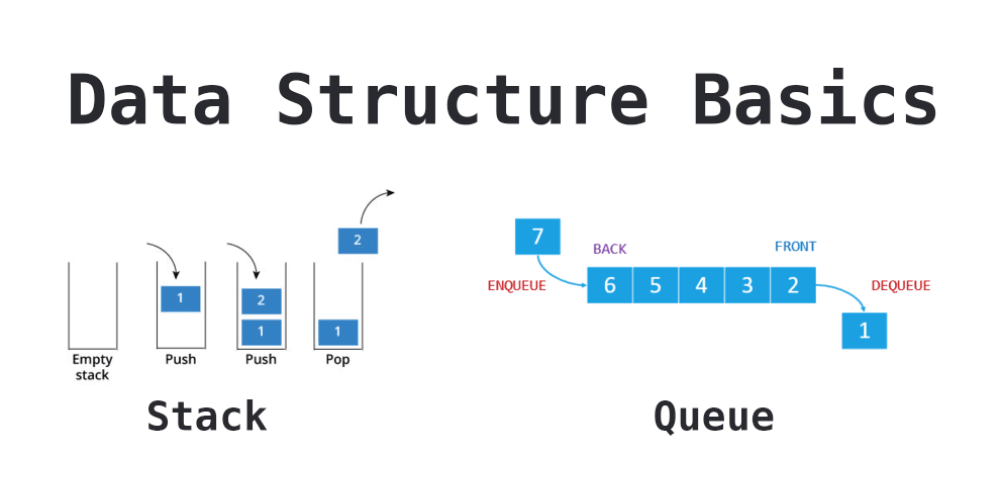
스택과 큐의 차이
스택
가장 마지막으로 들어간 데이터가 가장 첫 번째로 나오는 성질( LIFO, Last In First Out) 삽입 및 삭제에 O(1), 탐색에 O(n)이 걸림. 재귀적인 함수, 알고리즘(dfs)에 사용되며 웹 브라우저 방문 기록 등에 쓰임.
#include<bits/stdc++.h>
using namespace std;
stack<int> stk;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
for(int i = 0; i < 10; i++)stk.push(i);
while(stk.size()){
cout << stk.top() << " ";
stk.pop();
}
}
/*
9 8 7 6 5 4 3 2 1 0
*/
큐
큐(queue)는 먼저 집어넣은 데이터가 먼저 나오는 성질(FIFO, First In First Out)을 지닌자료 구조, 삽입 및 삭제에 O(1), 탐색에 O(n)이 걸림. CPU 작업을 기다리는 프로세스, 스레드 행렬 또는 네트워크 접속을 기다리는 행렬, 너비우선 탐색, 캐시 등에 사용됩니다.
#include <bits/stdc++.h>
using namespace std;
int main(){
queue<int> q;
for(int i = 0; i < 10; i++)q.push(i);
while(q.size()){
cout << q.front() << " ";
q.pop();
}
return 0;
}
/*
0 1 2 3 4 5 6 7 8 9
*/
그래프와 트리, 그리고 BST
그래프
그래프는 정점과 간선으로 이루어진 자료 구조
트리
트리는 그래프 중 하나로 그래프의 특징처럼 정점과 간선으로 이루어져 있고, 트리 구조로 배열된 일종의 계층적 데이터의 집합, 트리의 특징은 다음과 같다.
1. 부모, 자식 계층 구조를 가집니다.
2. V - 1 = E라는 특징이 있습니다. 간선 수는 노드 수 - 1입니다.
3. 임의의 두 노드 사이의 경로는 ‘유일무이’하게 ‘존재’합니다. 즉, 트리 내의 어떤 노드와 어떤
노드까지의 경로는 반드시 있습니다.
이진트리
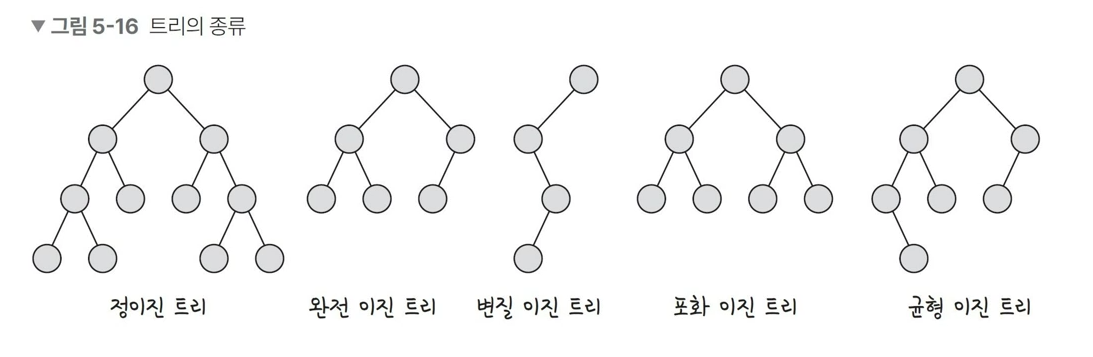
이진트리는 자식의 노드 수가 두 개 이하인 트리를 의미하며, 이를 다음과 같이 분류
- 정이진 트리(full binary tree) : 자식 노드가 두 개인 이진트리를 의미
- 완전이진트리(complete binary tree) : 왼쪽에서부터 채워져 있는 이진 트리를 의미, 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 경우 왼쪽부터 채워져 있음
- 변질 이진 트리(degenerate binary tree) : 자식 노드가 하나밖에 없는 이진트리를 의미
- 포화 이진 트리(perfect binary tree) : 모든 노드가 꽉차있는 이진 트리를 의미
- 균형 이진 트리(balanced binary tree) : 왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진트리를 의미
map, set을 구성하는 레드 블랙 트리는 균형 이진 트리 중 하나임
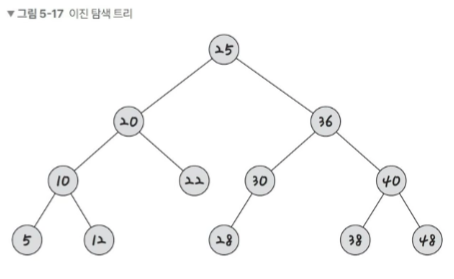
이진 탐색 트리(BST : Binary Search Tree)
이진 탐색 트리(BST)는 노드의 오른쪽 하위 트리에는 ‘노드 값보다 큰 값’이 있는 노드만 포함되고, 왼쪽 하위 트리에는 ‘노드 값보다 작은 값’이 들어 있는 트리를 말합니다
"검색"에 용이
선형적인 트리가 된다면 굉장히 비효율적
균형잡힌 트리 : AVL 트리, 레드블랙트리
둘 다 삽입, 탐색, 삭제 O(logN) 시간복잡도.
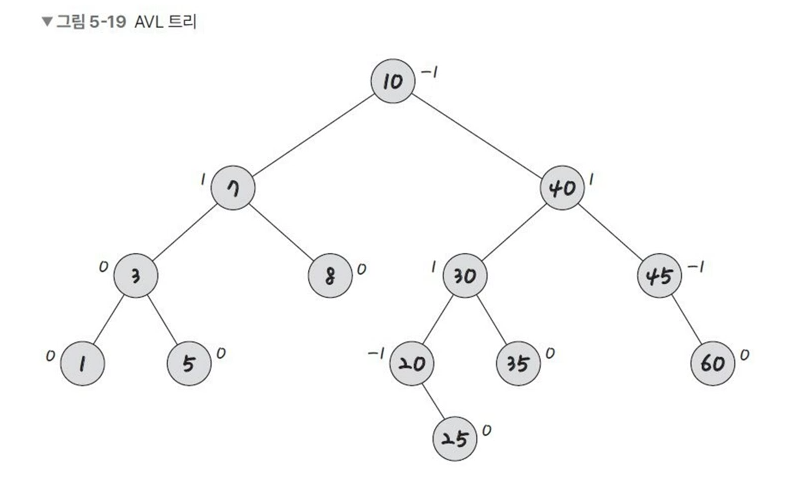
- AVL 트리(Adelson-Velsky and Landis tree) : 균형이 안 맞는 것을 맞추기 위해 트리 일부를 왼쪽 혹은 오른쪽으로 회전시키며 균형을 잡음.(선형적인 트리 방지)
특징 : 두 자식 서브트리의 높이는 항상 최대 1만큼 차이 남 (균형적)
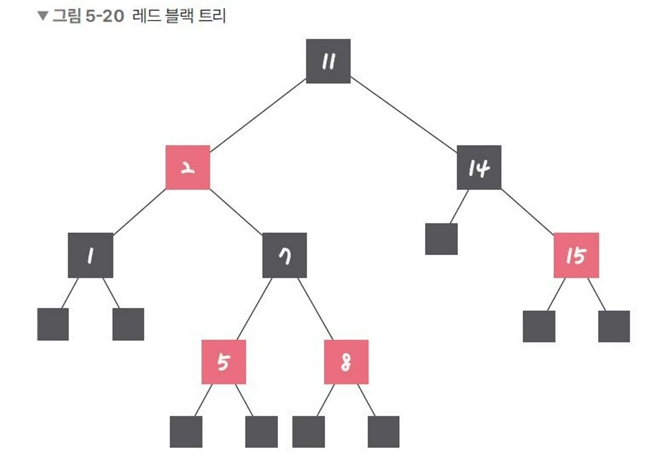
- 레드 블랙 트리 : C++ STL의 set, multiset,map, and multimap이 이 레드 블랙 트리를 이용하여 구현되어 있음. “모든 리프 노드와 루트 노드는 블랙이고 어떤 노드가 레드이면 그 노드의 자식은 반드시 블랙”이다 라는 특징을 가짐.
각 노드는 빨간색 또는 검은색 색상을 나타내는 추가 비트를 저장하고 이를 통해 삽입 및 삭제 중에 트리가 균형을 유지하는데 사용됨
즉, C++ STL의 set, multiset, map, multimap은 모두 레드블랙 트리를 이용하여 구현해서, 탐색, 삽입, 삭제가 모두 O(log n)임
해시테이블
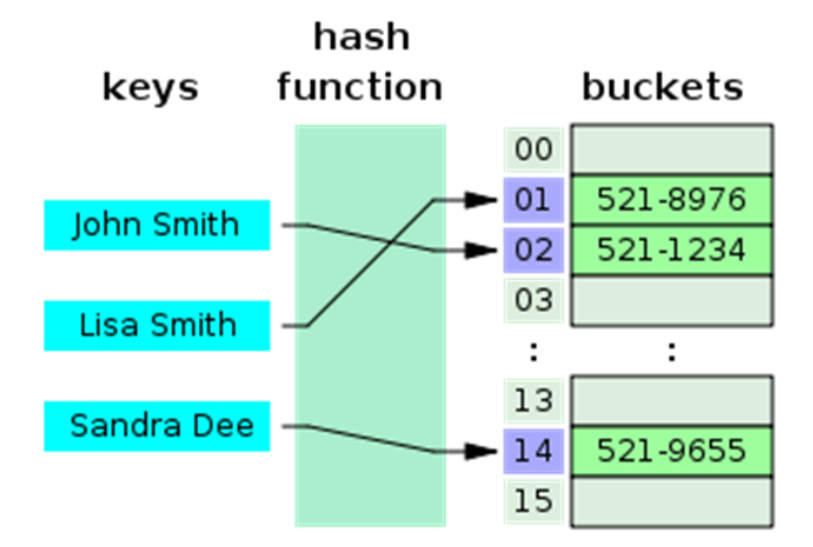
해시 테이블은 무한에 가까운 데이터들을 유한한 개수의 해시 값으로 매핑한 테이블입니다. 삽입, 삭제, 탐색 시 평균적으로 O(1)의 시간 복잡도를 가지며 최악의 경우 O(n)의 시간복잡도를 가집니다.
(C++에서는 unordered_map으로 구현됨.)
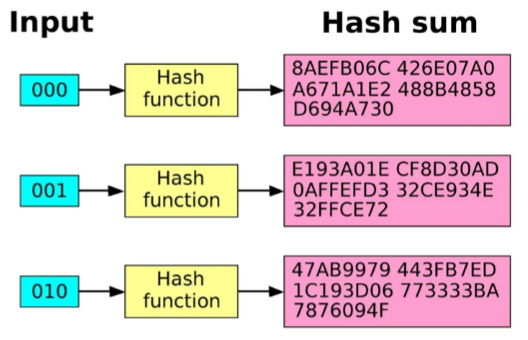
- 해시 : 다양한 길이를 가진 데이터를 고정된 길이를 가진 데이터로 매핑(mapping)한 값
- 해싱 : 임의의 데이터를 해시로 바꿔주는 일이며 해시 함수가 이를 담당
- 해시 함수 : 임의의 데이터를 입력으로 받아 일정한 길이의 데이터로 바꿔주는 함수
#include <bits/stdc++.h>
using namespace std;
int v[10];
int main(){
unordered_map<string, int> umap;
umap["test1"] = 4;
umap["test2"] = 10;
for(auto element : umap){
cout << element.first << " :: " << element.second << '\n';
}
cout << umap["test1"] << "\n";
return 0;
}
/*
test5 :: 5
test1 :: 4
not found..
5
2
1
*/
해시테이블과 충돌문제(collision)
해시충돌문제 발생? 당연히 해시값이 “똑같은값"이 발생할 때 충돌이 발생됨.
매우 큰 테이블이라도 birthday paradox에 의해 충돌이 발생될 확률은 높습니다.
예를 들어 같은 방에 생일이 같은 사람이 두 명 이상 있을 확률이 50%가 되려면 방에 23명밖에 없어도 됩니다.
https://www.geeksforgeeks.org/birthday-paradox/
Birthday Paradox - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
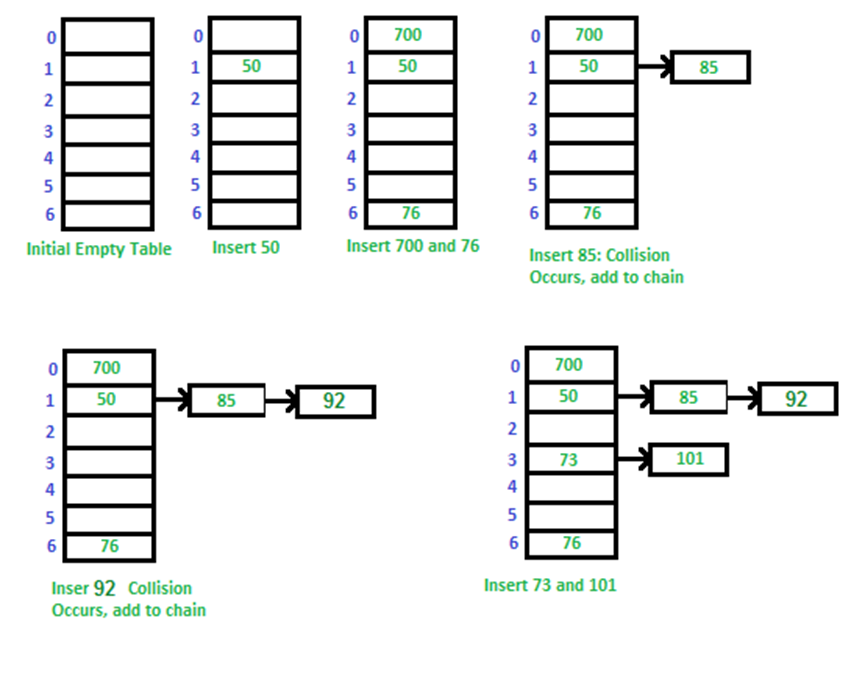
체이닝(Chaining)
충돌시 연결리스트에 할당, 충돌시 연결리스트 탐색.
장점: 구현간단, 해시테이블에 많은 데이터를 집어넣을 수 있음.
단점 : 연결리스트기반이라 캐시성능이 좋지 않다. 체인이 길어지면 최악의 경우 O(n)이 될 수 있음.
다음그림 : key mod 7이라면?
이 때 연결리스트 뿐만 아니라 동적배열, 균형잡힌 트리인 레드블랙트리가 사용되며 Java 8 이상에서는 레드 블랙트리를 HashMap에 사용합니다.
JEP 180: Handle Frequent HashMap Collisions with Balanced Trees
JEP 180: Handle Frequent HashMap Collisions with Balanced Trees AuthorMike DuigouOwnerBrent ChristianTypeFeatureScopeImplementationStatusClosed / DeliveredRelease8Componentcore-libsDiscussioncore dash libs dash dev at openjdk dot java dot netEffortMDur
openjdk.org
개방 주소법(Open Addressing)
충돌시 다른 버켓에 데이터를 삽입
- 선형 탐색(Linear Probing): 해시충돌 시 다음 버켓, 혹은 몇 개를 "선형적으로” 건너뛰어 데이터를 삽입한다.
- 제곱 탐색(Quadratic Probing): 해시충돌 시 제곱만큼 건너뛴 버켓에 데이터를 삽입(1,2,4,8..)
- 이중 해시(Double Hashing): 해시충돌 시 다른 해시함수를 한 번 더 적용한 결과를 이용해서 데이터를 삽입

해시테이블과 이중연결리스트로 LRU 페이지 교체 알고리즘 구현하기
LRU : 참조가 가장 오래된 페이지를 바꾸는 알고리즘 (운영체제 관련)
- 원래는 오래된 것을 파악하기 위해 계수기, 스택을 두어야 함.
오래된 것 : 리스트의 가장 마지막 요소 / 최근에 참조된 것 : 리스트의 가장 첫번째 요소
자 그렇다면 페이지가 들어왔을 때 해당 페이지가 캐시에 있는지를 확인하는(탐색) 로직을 연결리스트로만 구현하면 ? O(n) , 탐색의 시간복잡도가 낮은 자료구조 : 배열, 해시테이블 이 중에서 배열은 find라는 함수가 없음.(C++ 자료구조상)따라서 해시테이블을 하는게 더 편함.
해당 로직을 해시테이블로 구현하자.
#include <bits/stdc++.h>
using namespace std;
//list는 캐시를 뜻함.
//hash는 들어왔을 때
//해당 페이지가 있는지 없는지를
//빠르게 체크해서 해당부분을 erase하는 역할을 함.
class LRUCache {
list<int> li;
unordered_map<int, list<int>::iterator> hash;
int csize;
public:
LRUCache(int);
void refer(int);
void display();
};
LRUCache::LRUCache(int n){
csize = n;
}
void LRUCache::refer(int x){
//해시에 들어오는 페이지에 해당하는 값이 없을 때
if (hash.find(x) == hash.end()) {
if (li.size() == csize) {
// 가장 끝에 있는 것을 뽑아낸다.
// 이는 가장 오래된 것을 의미한다.
int last = li.back();
li.pop_back();
hash.erase(last);
}
}else {
cout << "지웁니당! : " << distance(li.begin(), hash[x]) << "번째 " << *hash[x] << '\n';
li.erase(hash[x]);
}
// 해당 페이지를 참조할 때
// 가장 앞에 붙인다. 또한 이를 해시테이블에 저장한다.
li.push_front(x);
hash[x] = li.begin();
}
void LRUCache::display(){
for (auto it = li.begin(); it != li.end(); it++){
cout << (*it) << " ";
}
cout << "\n";
}
int main(){
LRUCache ca(3);
ca.refer(1);
ca.display();
ca.refer(3);
ca.display();
ca.refer(0);
ca.display();
ca.refer(3);
ca.display();
ca.refer(5);
ca.display();
ca.refer(6);
ca.display();
ca.refer(3);
ca.display();
return 0;
}
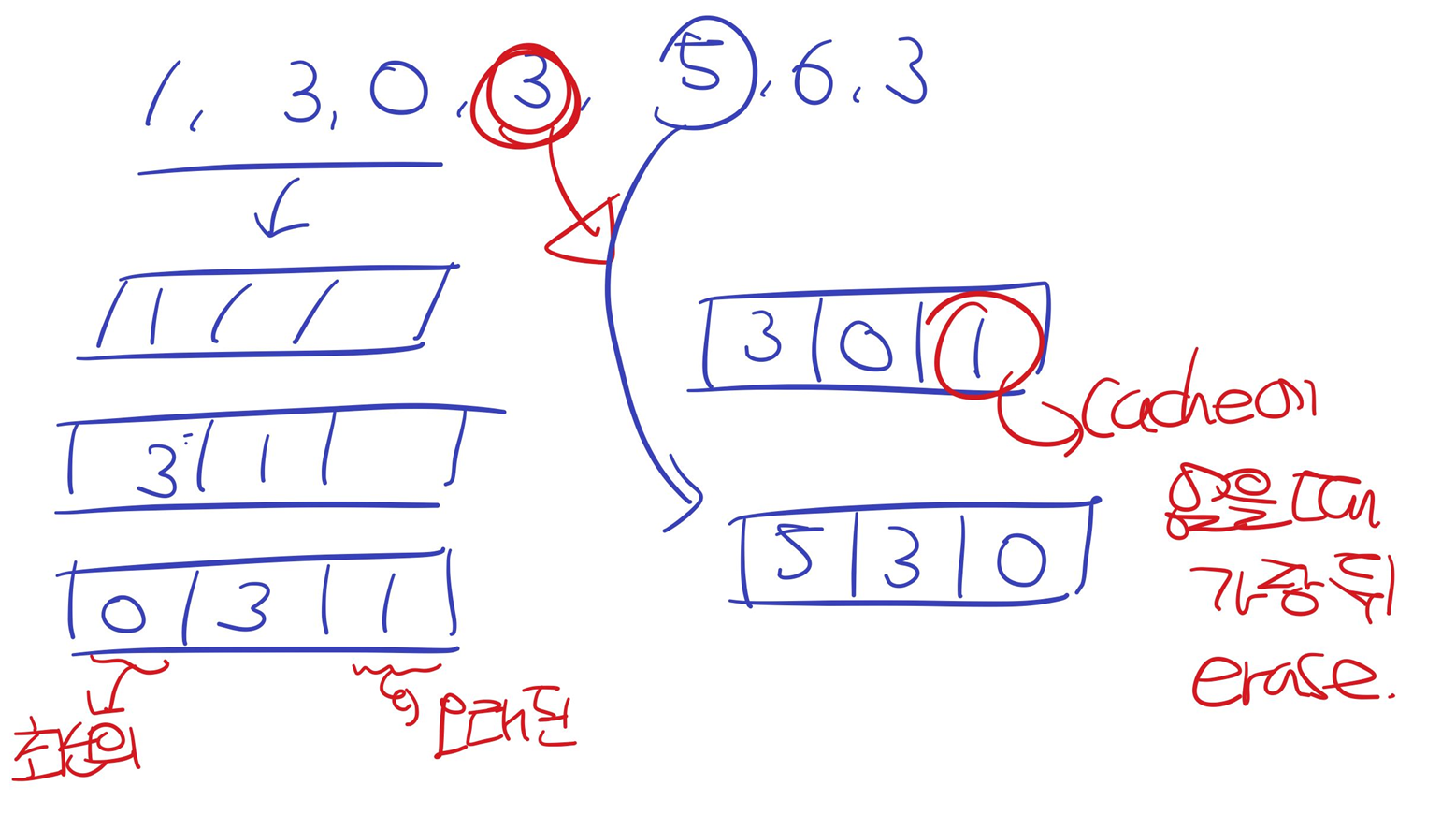
/*
1
3 1
0 3 1
3 0 1
5 3 0
6 5 3
3 6 5
*/

Q. 로또번호 7개를 셔플하기 위한 가장 좋은 자료구조는?
필요한 로직 : 셔플 : 탐색 + swap
- 삽입이나 삭제가 필요하지 않다.
- sequence 적인 자료구조는 배열, 연결리스트
- 이중에서 탐색에 O(1)인 배열을 사용하는 것이 좋다.
- 실질적 로직 : 랜덤 인수 + swap
// 코드설명 : Initialize random number generator seed + swap
#include<bits/stdc++.h>
using namespace std;
void swap (int *a, int *b){
int temp = *a;
*a = *b;
*b = temp;
}
void printArray (int arr[], int n){
for (int i = 0; i < n; i++) cout << arr[i] << " ";
cout << "\n";
}
void randomize (int arr[], int n){
// 프로그램 실행할 때 마다 다른 값이 나타나도록 seed를 주어야 함.
srand (time(NULL));
for (int i = n - 1; i > 0; i--){
int j = rand() % (i + 1);
swap(&arr[i], &arr[j]);
}
}
int main(){
int arr[] = {1, 2, 3, 4, 5, 6, 7};
int n = sizeof(arr) / sizeof(arr[0]);
randomize (arr, n);
printArray(arr, n);
return 0;
}
출처 : 면접을 위한 CS 전공지식 노트
'CS > 자료구조' 카테고리의 다른 글
| 자료구조 면접 질문 (1) | 2022.09.28 |
|---|---|
| <자료구조> 우선순위 큐 (0) | 2022.04.20 |
| <자료구조> queue와 deque (0) | 2022.04.19 |
| <자료구조> stack (0) | 2022.04.19 |
| <자료구조> set과 multiset (0) | 2022.04.19 |


