이번주차는 그래프이론과 DFS(깊이우선탐색), BFS(너비우선탐색) 그리고 트리순회인 preorder, inorder, postorder를 다루겠습니다.
그래프이론
그래프이론은 오일로경로, SCC, 단절점 등의 어려운 개념들도 많고 넓은 범위를 다루는 이론이지만 이 주차에서는 코딩테스트에 자주 나오며 그래프이론의 기본을 배워보겠습니다.
정점과 간선
"어떠한 곳이나 어떠한 사람"으로 부터 "무언가로 간다"라고 했을 때 "어떠한 곳이나 어떠한 사람"은 정점(Vertex)이 되고 "무언가로 간다"는 간선(Edge)이 됩니다.
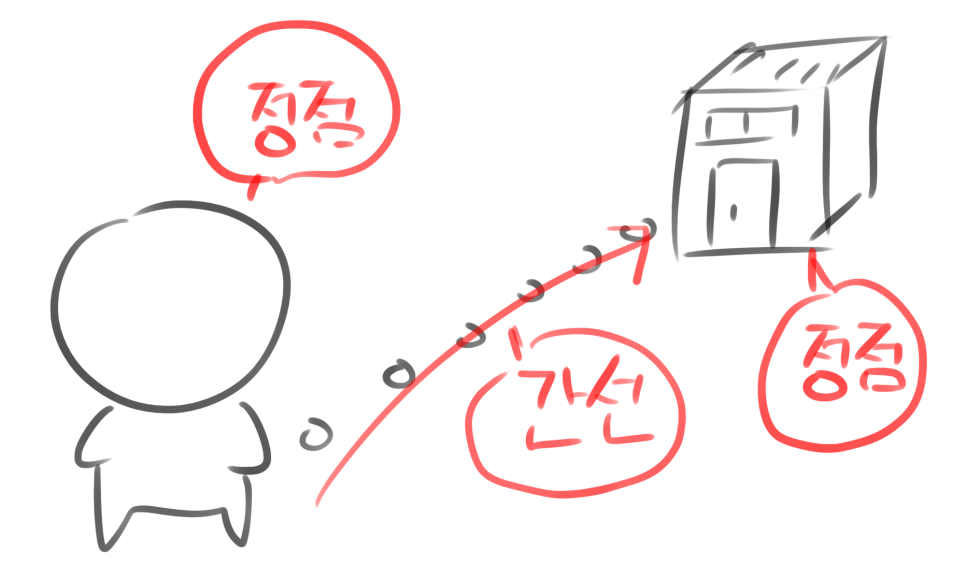
필자가 위 그림처럼 어떤 아파트로 간다고 해봅시다. 저와 아파트는 하나의 정점이고 거기로 가는 길은 간선이 됩니다.

필자가 어떤 사람을 좋아한다고 해봅시다. 필자와 어떤 사람은 정점이 이러한 마음은 간선이 됩니다. 자 이 때 제가 만약에 어떤 사람을 좋아하는데 어떤 사람은 저를 좋아하지 않는 "짝사랑"이라고 해봅시다. 이것은 어떠한 간선일까요? 바로 단방향 간선입니다. 저의 마음만이 그 사람으로 가는 길밖에 없는 슬픈 관계이지요.

하지만 그 어떤 사람도 저를 좋아한다면 어떻게 될까요? 바로 양방향 간선이 됩니다. 저의 마음도 그 어떤 사람의 마음도 갈 수 있는 "사랑"이라 불리는 상태인 것이죠.
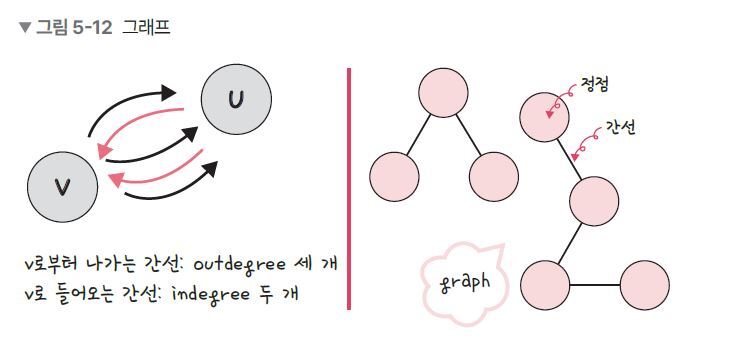
정점으로 나가는 간선을 해당 정점의 outdegree라고 하며 들어오는 간선을 해당정점의 indegree라고 합니다. 해당 정점은 outdegree는 3개 indegree는 2개인 상태입니다. 또한 정점은 약자로 V또는 U라고 하며 보통 어떤 정점으로부터 시작해서 어떤 정점까지를 간다를 "U에서부터 V로 간다" 라고 표현을 합니다. 지금까지 설명한 정점과 간선들로 이루어진 집합을 "그래프(Graph)"라고 합니다.
가중치
간선과 정점사이에 드는 비용을 뜻합니다. 1번노드와 2번노드까지 가는 비용이 한칸이라면 1번노드에서 2번노드까지의 가중치는 한칸입니다.
예를 들어 제가 성남이라는 정점에서 네이버라는 정점까지 걸리는 택시비가 13000원이라면 성남에서 네이버까지 가는 가중치는 13000원이 됩니다.
트리
트리는 그래프 이론에서 사이클이 없는 무방향 그래프 또는 사이클이 없는 방향그래프인 DAG(Directed Acyclic Graph)를 지칭합니다.
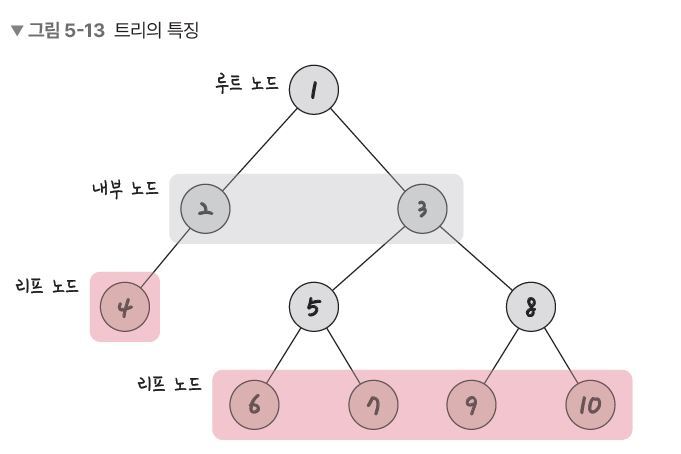
트리는 그래프의 일종이며 다음 특징을 가진다는 점이 다릅니다.
1. 부모, 자식 계층 구조를 가집니다. 지금 보면 5번 노드는 6번 노드와 7번 노드의 부모 노드이고, 6번노드와 7번 노드는 5번 노드의 자식 노드입니다. 같은 경로 상에서 어떤 노드보다 위에 있으면 부모,아래에 있으면 자식 노드가 됩니다.
2. V - 1 = E라는 특징이 있습니다. 간선 수는 노드 수 - 1입니다.
3. 임의의 두 노드 사이의 경로는 ‘유일무이’하게 ‘존재’합니다. 즉, 트리 내의 어떤 노드와 어떤 노드까지의 경로는 반드시 있습니다.
루트노드
가장 위에 있는 노드를 뜻합니다. 보통 트리문제가 나오고 트리를 탐색할 때 루트노드를 중심으로 탐색을 하면 문제가 쉽게 풀리는 경우가 많습니다.
내부노드
루트노드와 내부노드 사이에 있는 노드를 뜻합니다.
리프노드
실제 알고리즘 고인물과 카톡한 내용입니다. 아래그림처럼 리프노드는 자식노드가 없는 노드를 뜻합니다.
트리의 높이와 레벨
다음 그림은 트리의 높이와 레벨을 설명한 그림입니다.
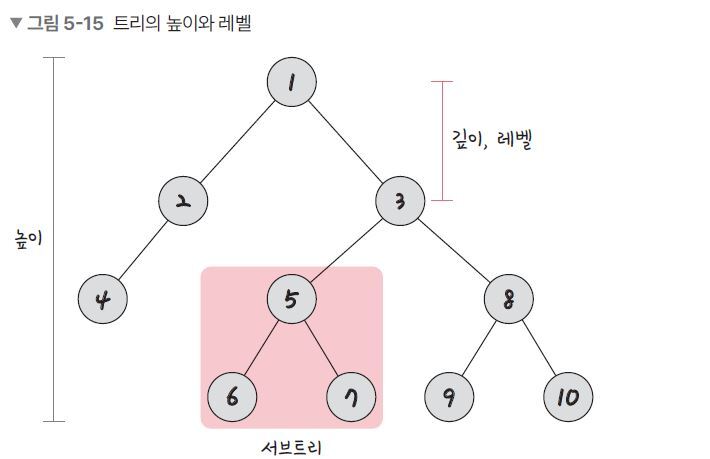
- 깊이: 트리에서의 깊이는 각각의 노드마다 다르며 루트 노드에서 특정 노드까지 최단거리로 갔을 때의 거리를 말합니다. 예를 들어 4번 노드의 깊이는 2입니다.
- 높이: 트리의 높이는 루트 노드부터 리프 노드까지의 거리 중 가장 긴 거리를 의미하며 앞 그림의 트리 높이는 3입니다.
- 레벨: 트리의 레벨은 주어지는 문제마다 조금씩 다르지만 보통 깊이와 같은 의미를 지닙니다. 1번 노드를 0레벨이라고 하고 2번 노드, 3번 노드까지의 레벨을 1레벨이라고 할 수도 있고, 1번 노드를 1레벨이라고도 할 수 있습니다. 예를 들어 1번 노드를 1레벨이라고 한다면 2번 노드와 3번 노드는 2레벨이 됩니다.
- 서브트리: 트리 내의 하위 집합을 서브트리라고 합니다. 트리 내에 있는 부분집합이라고도 보면 됩니다. 지금 보면 5번, 6번, 7번 노드가 이 트리의 하위 집합으로 "저 노드들은 서브트리다"라고 합니다.
이진트리
자식의 노드 수가 2개 이하인 트리를 의미하며 이를 다음과 같이 분류합니다.
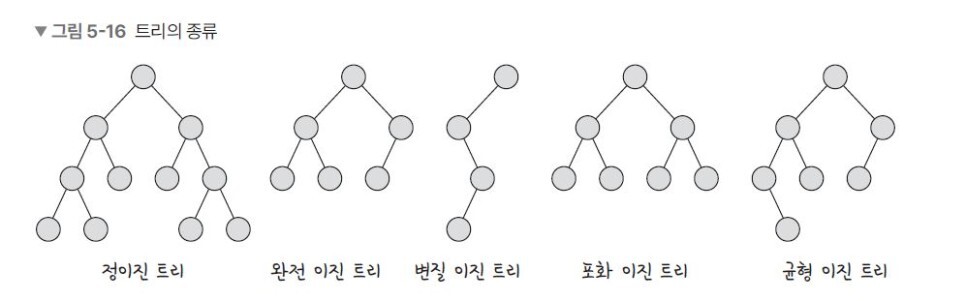
- 정이진 트리(full binary tree): 자식 노드가 0 또는 2개인 이진 트리를 의미합니다.
- 완전 이진 트리(complete binary tree): 왼쪽에서부터 채워져 있는 이진 트리를 의미합니다. 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있으며 마지막 레벨의 경우 왼쪽부터 채워져 있습니다.
- 변질 이진 트리(degenerate binary tree): 자식 노드가 하나밖에 없는 이진 트리를 의미합니다.
- 포화 이진 트리(perfect binary tree): 모든 노드가 꽉 차 있는 이진 트리를 의미합니다.
- 균형 이진 트리(balanced binary tree): 왼쪽과 오른쪽의 노드의 높이 차이가 1이하인 이진 트리를 의미합니다. map, set을 구성하는 레드블랙트리는 균형이진트리 중 하나입니다.
이진탐색트리
다음 그림은 이진탐색트리입니다.
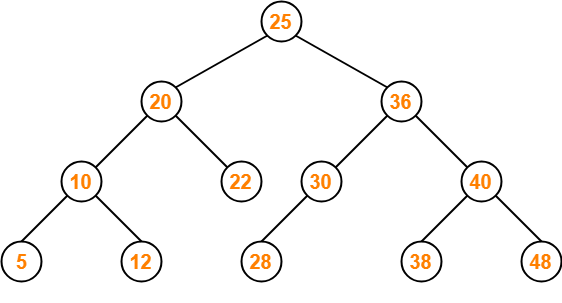
노드의 오른쪽 하위 트리에는 "노드의 값보다 큰 값"이 있는 노드만 포함되고 왼쪽 하위트리에는 "노드의 값보다 작은값"이 들어있는 트리를 말합니다. 이 때 왼쪽 및 오른쪽 하위 트리도 해당 특성을 가집니다. 이렇게 두면 "검색"을 하기에 용이합니다. 왼쪽에는 작은 값, 오른쪽에는 큰 값이 이미 정해져있기 때문에 예를 들어 10을 찾으려고 한다면 25의 왼쪽 노드들만 찾으면 된다는 것은 자명하기 때문입니다. 이렇게 한다면 전체탐색을 하지 않아도 되겠죠?
숲
트리로 이루어진 집합을 숲(forest)이라고 합니다.
DAG
DAG(DAG, Directed Acyclic Graph) 는 방향성이 있고 사이클이 없는 그래프를 말합니다.

추후 DP를 배울 때 무조건 DAG를 만들어서 합니다. 예를 들어 문제에서 양방향 그래프로 주어졌고 이 해당 그래프에서 DP를 해야한다면 그냥 할 것이 아니라 DAG를 만들어서 해야합니다.
연결된 컴포넌트
연결된 컴포넌트(connected component)는 연결되어있는 정점과 간선의 집합을 말합니다.

위 그림의 연결된 컴포넌트의 수는 몇개일까요? 2개, 3개, 2개입니다. 즉, 연결되어있는지 아니면 연결되어있지 않는지를 토대로 연결된 컴포넌트로 나눕니다. 이러한 컴포넌트들을 번호를 붙여가며 색칠하는 알고리즘은 풀르드필(floodfill)이라고 합니다.
그래프표현방법
컴퓨터에게 내가 이러한 그래프를 그렸다고 알려줄 표현방법으로는 인접행렬과 인접리스트가 있습니다.
인접행렬
인접행렬이란 그래프에서 정점과 간선의 관계를 나타내는 정사각형 행렬을 의미합니다. 보통 불리언2차원행렬을 쓰며 예를 들어 2차원배열 a[1004][1004]가 정의되어있을 때 a[1][3] = 1이라는 뜻은 1로부터 3까지 가는 경로가 있다는 의미를 말하며 a[1][2] = 0이라면 1로부터 2까지 가는 경로가 없다는 것을 의미합니다.
bool a[1004][1004];
for(int i = 0;i < V; i++){
for(int j = 0; j < V; j++){
if(a[i][j]){
cout << i << "부터 " << j << "까지 경로가 있습니다.\n";
}
}
}위 코드는 a[i][j], 즉 i로부터 j까지 경로가 있다면 "i부터 j까지 경로가 있습니다."를 출력하는 코드입니다. 이렇게 2중 반복문을 통해 쓰입니다. 시간복잡도는 O(V^2), 공간복잡도 또한 O(V^2)입니다.
Q. 3번노드에서 5번노드로 가는 경로가 있고 이를 인접행렬로 표현한다면 어떻게 될까요?
a[3][5] = 1;
인접리스트
인접 리스트(adjacency list)는 그정점에서 정점을 연결하는 것을 하나의 연결 리스트를 통해 표현하는 것을 의미합니다.
vector<int> adj[1004];
adj[1].push_back(2);
for(int i = 0;i < V; i++){
for(int there : adj[i]){
}
//위와 아래 코드는 의미가 같습니다.
for(int j = 0; j < adj[i].size(); j++){
int there = adj[i][j];
}
}보통 인접리스트는 벡터(vector) 여러개를 이용해서 인접한 노드들을 그 vector에 담습니다. adj[1].push_back(2)는 1번노드로부터 2번노드로 갈 수 있음을 의미합니다.
for(int there : adj[i]){
}
//위와 아래 코드는 의미가 같습니다.
for(int j = 0; j < adj[i].size(); j++){
int there = adj[i][j];
}위와 아래는 같은 코드입니다. 어떠한 i라는 노드로부터 연결되어있는 정점들을 탐색하는 것인데 위코드처럼 숏컷을 써서 해야 빠르고 디버깅이 쉽습니다.
Q. 3번노드로부터 5번 노드로 갈 수 있는 것을 어떻게 구현해야할까요?
adj[3].push_back(5);
인접리스트는 시간복잡도는 O(V + E), 공간복잡도 또한 O(V + E)입니다.
자 그럼 이 둘 중 어떤 것을 써야 할까요?
보통 인접리스트로 할 생각을 하고 문제에서 만약에 인접행렬로 주어졌다면 인접행렬로 푸는 것이 좋습니다.
탐색방법
그래프는 2차원 배열인 맵으로 주어지고 4가지 방향을 탐색하라고 할 때도 있고 노드와 노드 사이의 인접리스트로 주어질 때도 있습니다. 이 2가지 경우에 대해 어떻게 "탐색"을 해야 하는지를 알아보겠습니다.
2차원배열인 맵으로 주어지고 4가지 방향탐색
어떠한 y, x가 주어졌을 때 y, x를 중심으로 상하좌우 4가지 방향으로 탐색은 어떻게 하는 것일까요?
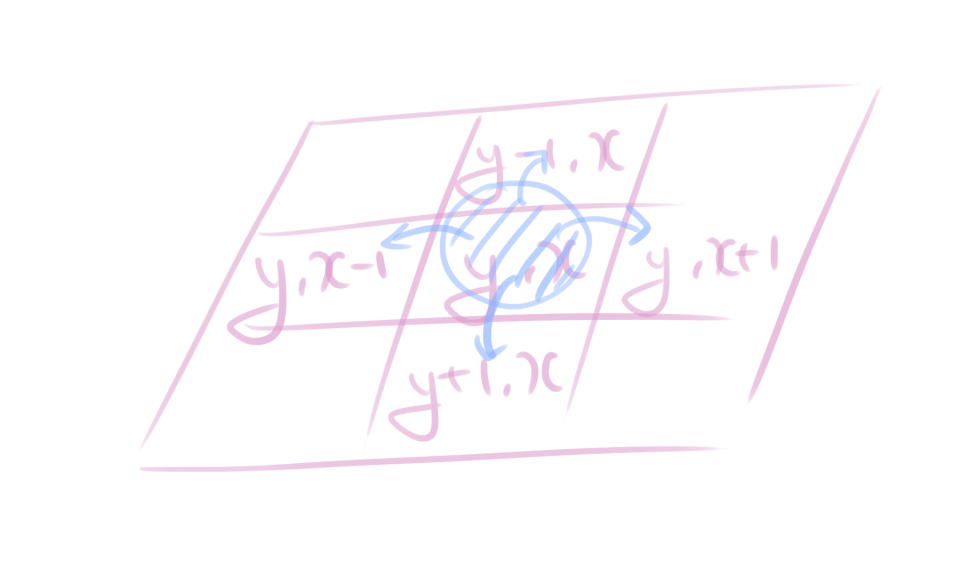
어떠한 노드가 있습니다. 여기서 4가지 방향인 위, 아래, 왼쪽, 오른쪽 방향은 위 그림처럼 되겠죠? 지금 보시면 어떠한 노드에서 보았을 때 y좌표에 -1 또는 x좌표에 +1 등을 하면서 탐색을 할 수 있는 것을 볼 수 잇습니다. 예를 들어 제가 {1, 1} 인데 여기서 오른쪽으로 이동한다? 어떻게 될까요? {1, 2}가 됩니다. 아래쪽으로 이동한다면 {2, 1}이 됩니다. 이렇게 +1 또는 -1이 y, x좌표에 추가된다는 것을 알 수 있는데 이를 보통 방향벡터를 정의해서 구현합니다.
자 제가 정의한 방향벡터입니다. 위쪽방향부터 시계방향으로 상하좌우방향에 대한 방향벡터를 구현했습니다.
const int dy[] = {-1, 0, 1, 0};
const int dx[] = {0, 1, 0, -1};자 이렇게 하면 {y-1, x}, {y, x + 1} ... 를 구현할 수 있겠죠? 어떠한 y, x 좌표로부터 이부분에 대한 것을 +를 해주기만 하면 4방향 탐색이 완료됩니다.
Q1. 맵은 y는 0이상 1000미만 , x는 0이상 1000 미만 의 좌표를 가집니다. {1, 1}좌표에서 4방향을 출력하시오.
#include <bits/stdc++.h>
using namespace std;
int a[1004][1004];
const int dy[] = {-1, 0, 1, 0};
const int dx[] = {0, 1, 0, -1};
int main(){
int y = 1;
int x = 1;
for(int i = 0; i < 4; i++){
int ny = y + dy[i];
int nx = x + dx[i];
cout << ny << " : " << nx << '\n';
//탐색
}
return 0;
}
/*
0 : 1
1 : 2
2 : 1
1 : 0
*/이렇게 y, x를 중심으로 ny, nx, 내가 지금 가야할 곳을 정의해서 로직이 구축되겠죠? 위 코드는 {1, 1} 에서 4개의 방향을 탐색하는 코드입니다. 지금 보시는 dy, dx를 기반으로 ny, nx를 정의하죠. 저 dy, dx를 방향벡터라고 합니다. 어떠한 y, x로부터 더해지는 방향을 뜻합니다. 이 dy, dx를 통해 내가 지금 탐색해야할 곳인 다음 지점인 ny와 nx를 정의해서 탐색하는 것을 볼 수 있습니다. 자 그렇다면 8가지의 방향이라면 어떻게 해야할까요? 거기에 따라 dy, dx를 다시 정의하고 for문으로 8까지 순회해야겠죠?
Q2. 맵은 y는 0 이상 1000미만 , x는 0이상 ~ 1000미만의 좌표를 가집니다. {0, 0}좌표에서 4방향 중 맵에 벗어나지 않는 것을 출력하시오.
#include <bits/stdc++.h>
using namespace std;
int a[1004][1004];
const int dy[] = {-1, 0, 1, 0};
const int dx[] = {0, 1, 0, -1};
int main(){
int y = 0;
int x = 0;
for(int i = 0; i < 4; i++){
int ny = y + dy[i];
int nx = x + dx[i];
if(ny < 0 || ny >= 1000 || nx < 0 || nx >= 1000) continue;
cout << ny << " : " << nx << '\n';
}
/*
0 : 1
1 : 0
*/
return 0;
}자 이 코드는 4방향을 탐색하라고 했더니 2개밖에 출력되지 않는 걸 볼 수 있습니다.
이 코드는 틀린 걸까요?
if(ny < 0 || ny >= 1000 || nx < 0 || nx >= 1000) continue;우리가 맵을 탐색할 때 주의해야할 점이 있습니다. 주어진 맵을 벗어나면 안되기 때문입니다. 맵을 0이상 ~ 1000 미만으로 정의를 해놓았는데 그 밖을 벗어나면 배열 인덱싱에러가 나타나겠죠? 언더플로우와 오버플로우 에러를 이렇게 방지해줍시다. 맵을 탐색할 떄는 이렇게 항상 맵을 벗어나는지를 염두해두면서 위 코드처럼 작성해야 합니다.
노드와 노드 사이의 인접리스트 탐색
이 경우에는 어떠한 정점으로부터 연결된 지점을 there로써 정의하고 탐색해나가면 됩니다.
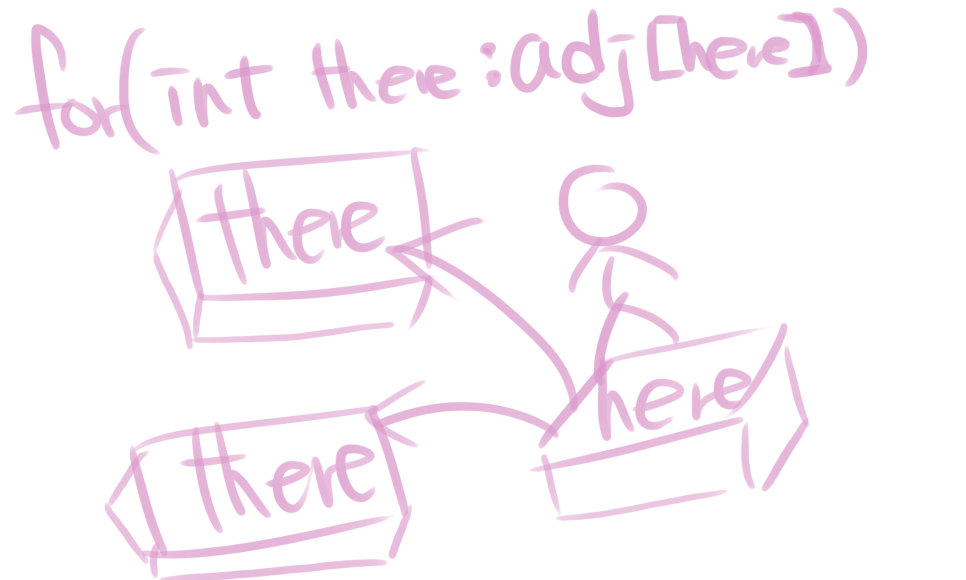
#include <bits/stdc++.h>
using namespace std;
vector<int> adj[1004];
int main(){
adj[1].push_back(2);
adj[1].push_back(3);
for(int there : adj[1]){
cout << there << " ";
}
return 0;
}
// 2 3먼저 인접리스트를 통해 1번 노드에 2번노드와 3번노드로 가는 길이 정해져있는 것을 볼 수 있죠? 1이라는 노드에서 이어진 노드들을 탐색하는 로직입니다. 지금 there에 2, 3이 찍히는 것을 볼 수 있습니다.
DFS, 깊이우선탐색
깊이 우선탐색은 그래프를 탐색할 때 쓰이는 알고리즘으로써 특정한 노드에서 가장 멀리 있는 노드를 먼저 탐색하는 알고리즘입니다.
주어진 맵전체를 탐색하며 한번 방문한 노드는 다시한번 방문하지 않기 때문에 만약 인접리스트로 이루어진 맵이면 O(V + E)이고 인접행렬의 경우 O(V^2)가 됩니다.
수도코드
DFS의 수도코드는 다음과 같습니다.
DFS(G, u)
u.visited = true
for each v ∈ G.Adj[u]
if v.visited == false
DFS(G,v)어떠한 정점 u의 visited를 참으로 바꾸고 u로부터 연결되어있는 v지점을 탐색합니다. 이 때 방문되어있지 않은 노드에 대해 재귀적으로 DFS를 호출합니다.

1번노드부터 시작해서 4번노드까지 멀리 떨어져있는 정점까지 먼저 방문한다음 그 다음 정점들을 방문하고 있습니다. 또한 방문한 정점은 다시 방문하지 않죠?
이 DFS를 구현하는 방법은 크게 2가지가 있습니다.
구현방법1
돌다리를 두들겨 보고 가는 방법입니다.

void dfs(int here){
visited[here] = 1;
for(int there : adj[here]){
if(visited[there]) continue;
dfs(there);
}
}만약 방문이 되어있다면(visited[there])이라면 방문을 하지 않고 방문이 안되어있다면 방문을 하는, 즉 해당 there에 대하여 dfs를 호출하는 방법입니다.
구현방법2
일단 호출하고 생각하는 방법입니다.

void dfs(int here){
if(visited[here]) return;
visited[here] = 1;
for(int there : adj[here]){
dfs(there);
}
}일단 방문되어있던 안되어있던 무조건 dfs를 호출하고 해당 함수에서 만약에 방문되어있다면 return 해 함수를 종료시키는 방법입니다.
문제에 따라 1번방법이 편할 떄도 2번방법이 편할 때도 있습니다. 둘 다 모두 자유롭게 구현할 줄 알아야 합니다.
예시문제. 종화는 방구쟁이야!

종화는 21세기 유명한 방구쟁이다. 종화는 방구를 낄 때 "이러다... 다 죽어!!" 를 외치며 방구를 뀌는데 이렇게 방귀를 뀌었을 때 방귀는 상하좌우 네방향으로 뻗어나가며 종화와 연결된 "육지"는 모두 다 오염된다. "바다"로는 방구가 갈 수 없다. 맵이 주어졌을 때 종화가 "이러다... 다 죽어!!"를 "최소한" 몇 번외쳐야 모든 맵을 오염시킬 수 있는지 말해보자. 1은 육지며 0은 바다를 가리킨다.
입력
맵의 세로길이 N과 가로길이 M 이 주어지고 이어서 N * M의 맵이 주어진다.
출력
"이러다... 다 죽어!!"를 몇번외쳐야하는지 출력하라.
범위
1 <= N <= 100
1 <= M <= 100
예제입력
예제출력
해설
이 문제는 어떤 문제일까요? 바로 앞서 설명한 연결된 컴포넌트(connected component)를 찾는 문제입니다.
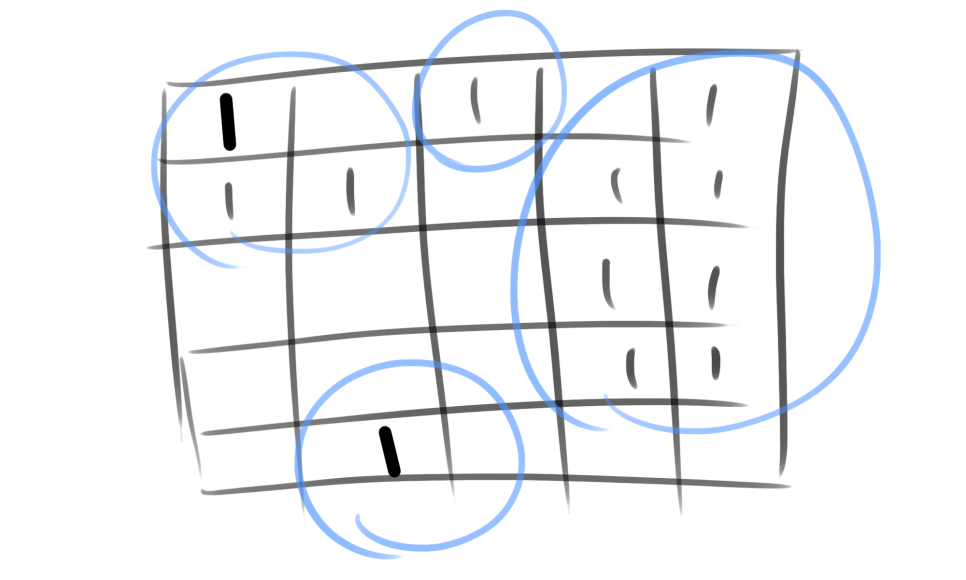
예제입력을 시각화했을 때 저렇게 묶은 부분이 바로 연결된 컴포넌트입니다.
정답코드
#include<bits/stdc++.h>
using namespace std;
int dy[4] = {-1, 0, 1, 0};
int dx[4] = {0, 1, 0, -1};
int m, n, k, y, x, ret, ny, nx, t;
int a[104][104];
bool visited[104][104];
void dfs(int y, int x){
visited[y][x] = 1;
for(int i = 0; i < 4; i++){
ny = y + dy[i];
nx = x + dx[i];
if(ny < 0 || nx < 0 || ny >=n || nx >= m) continue;
if(a[ny][nx] == 1 && !visited[ny][nx]){
dfs(ny, nx);
}
}
return;
}
int main(){
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cin >> a[i][j];
}
}
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(a[i][j] == 1 && !visited[i][j]){
ret++; dfs(i, j);
}
}
}
cout << ret << '\n';
return 0;
}상세설명
if(a[i][j] == 1 && !visited[i][j])
{
ret++; dfs(i, j);
}방문을 하지 않았고 육지라면 ret++를 하고 dfs를 호출합니다.
void dfs(int y, int x){
visited[y][x] = 1;
for(int i = 0; i < 4; i++){
ny = y + dy[i];
nx = x + dx[i];
if(ny < 0 || nx < 0 || ny >=n || nx >= m) continue;
if(a[ny][nx] == 1 && !visited[ny][nx]){
dfs(ny, nx);
}
}
return;
}메인이 되는 dfs입니다. 방문했다고 표기하고 4방향을 탐색하면서 dfs를 탐색해나갑니다.
Q. 이 문제를 풀 때 dfs가 퍼져나가는 것이 상상이 안된다면 이렇게 해보시는 것은 어떨까요?
#include<bits/stdc++.h>
using namespace std;
int dy[4] = {-1, 0, 1, 0};
int dx[4] = {0, 1, 0, -1};
int m, n, k, y, x, ret, ny, nx, t;
int a[104][104];
bool visited[104][104];
void dfs(int y, int x){
cout << y << " : " << x << '\n';
visited[y][x] = 1;
for(int i = 0; i < 4; i++){
ny = y + dy[i];
nx = x + dx[i];
if(ny < 0 || nx < 0 || ny >=n || nx >= m) continue;
if(a[ny][nx] == 1 && !visited[ny][nx]){
dfs(ny, nx);
}
}
return;
}
int main(){
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> m;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cin >> a[i][j];
}
}
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(a[i][j] == 1 && !visited[i][j]){
ret++; dfs(i, j);
}
}
}
cout << ret << '\n';
return 0;
}이 코드는 dfs 함수 내에 아래와 같은 코드를 집어넣었습니다.
cout << y << " : " << x << '\n';이렇게 y, x가 어떻게 뻗어나가는지를 보면서 이해를 하시는 것이 좋습니다.
BFS 너비우선탐색
BFS는 그래프를 탐색하는 알고리즘이며 노드에서 시작해 이웃한 노드들을 먼저 탐색하는 알고리즘이자 같은 가중치를 가진 그래프에서 최단거리알고리즘으로 쓰입니다. 시간복잡도는 DFS와 같으며 주어진 맵전체를 탐색하며 한번 방문한 노드는 다시한번 방문하지 않기 때문에 만약 인접리스트로 이루어진 맵이면 O(V + E)이고 인접행렬의 경우 O(V^2)가 됩니다.
참고로 가중치가 다른 그래프 내에서 최단거리 알고리즘은 다익스트라, 벨만포드 등을 써야 합니다.
수도코드1
BFS(G, u)
u.visited = true
q.push(u);
while(q.size())
u = q.front()
q.pop()
for each v ∈ G.Adj[u]
if v.visited == false
v.visited = true
q.push(v)먼저 시작지점인 u를 "방문처리"를 하고 "큐(queue)에 푸시"를 합니다. 그리고 q.size() 만큼 while 반복문을 돌면서 큐 앞단의 있는 u를 다시 끄집어내서 그 u를 중심으로 인접한 노드들을 탐색을 합니다. 방문한 정점은 다시 방문하지 않고 방문처리를 하면서 큐(queue)에 푸시를 하며 방문처리를 합니다.
수도코드2
BFS(G, u)
u.visited = 1
q.push(u);
while(q.size())
u = q.front()
q.pop()
for each v ∈ G.Adj[u]
if v.visited == false
v.visited = u.visited + 1
q.push(v)수도코드1의 경우 이론적인 성향이 강하고 이를 문제에서 풀 때 BFS를 구현할 때는 위코드와 같이 구축해야 합니다. 차이점은 v.visted = u.visited + 1로 최단거리 배열을 만드는 점입니다. 이 때 "시작지점이 다수" 라면 처음 큐에 푸시하는 지점도 다수가 되어야 하며 해당 지점들 모두 visited를 1로 만들면서 시작해야 합니다.
v.visited = u.visited + 1저 코드에서 비부분이 중요합니다. 내가 지금 가야할 곳에 지금 있는 곳에서 + 1을 하면서 최단거리배열(visited)을 만들어나가는 것입니다.
최단거리배열을 만들면서 진행을 하면 다음과 같이 레벨별로 탐색이 가능합니다.

2, 3, 4 는 레벨1 / 5, 6, 7, 8 은 레벨 2 / 9, 10, 11, 12는 레벨3 이렇게 레벨을 매길 수 있습니다. 어떻게 매길까요? 바로 최단거리배열(visited)을 통해서 매깁니다. 이 BFS의 핵심은 최단거리배열입니다. DFS와 똑같이 그래프를 탐색하는데 쓰일 수 있지만 차이점은 바로 이것입니다. "가중치가 같은 그래프"내에서 최단거리배열을 만들어놓으면 BFS는 "최단거리알고리즘"으로 쓰일 수가 있습니다.
수도코드를 보면서 어떻게 큐에 push가 되고 다시 pop이 되는지 한번 그림을 그려보면서 알아보도록 하겠습니다.
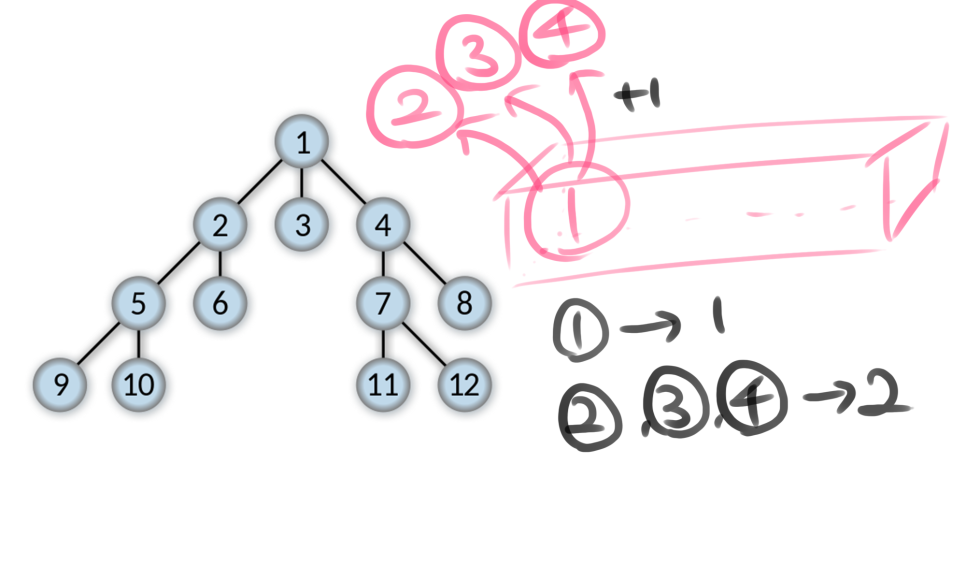
처음 1이라는 노드의 1을 기반으로 2, 3, 4라는 노드가 큐에 푸시가 됩니다. 그러면서 2, 3, 4에 해당하는 노드의 visited는 2라는 값을 가지게 됩니다.

다시 2, 3, 4라는 노드를 중심으로 5, 6, 7, 8 노드를 탐색하며 visited 배열을 +1하면서 갱신합니다.
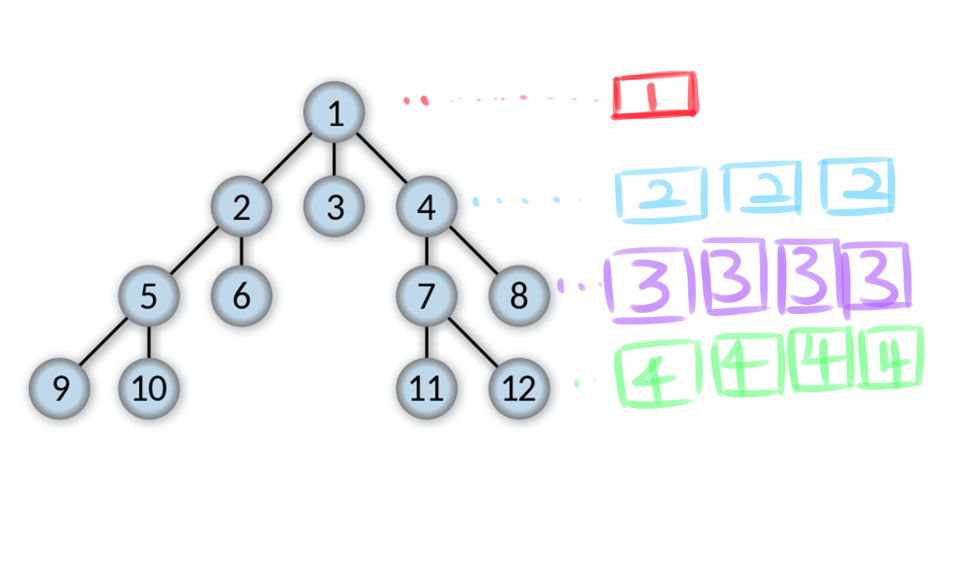
이렇게 해서 하다보면 위그림처럼 알록달록한 그림이 나오게 됩니다. 레벨별로 탐색할 수 있는 것을 볼 수 있죠? 이렇게 하면 최단거리로 쓸 수 있는 것입니다. 예를 들어 볼까요? 1번노드에서 9번노드로 가는 최단거리는 얼마일까요? 바로 4겠죠? 한칸지날때 한노드가 소모값이라면요.
Q. BFS는 가중치가 같은 그래프내에서만 최단거리 알고리즘으로 쓰이나요? 다른 그래프에서는 안되나요?
노드와 노드 사이에 한칸이 걸리는 그래프가 있다고 해봅시다. 여기서 1에서 5번으로 가는 최단거리는 얼마일까요?


위 그림처럼 2칸이 걸리게 됩니다. BFS로 레벨별로 탐색하기만 하면되죠.
하지만 가중치가 다른 그래프라면 어떨까요?
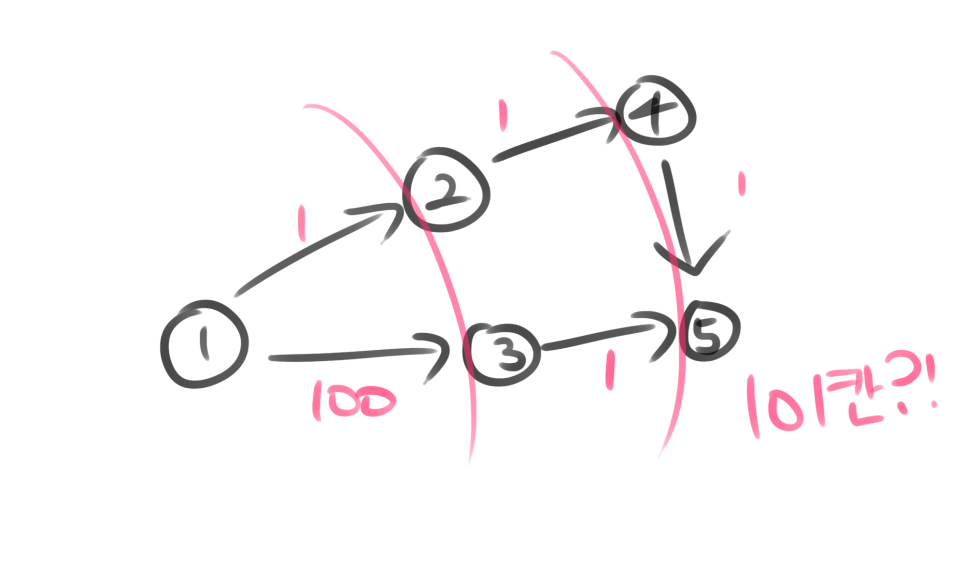
위처럼 되겠죠? 가중치가 다르지만 bfs를 썼더니 101칸이 나오는 것을 볼 수 있습니다. 원래는 3칸인데 말이죠. 즉, 가중치가 같을 때만 최단거리 알고리즘으로 쓸 수 있는 것을 볼 수 있습니다.
예시문제. 당근마킷 엔지니어 승원이

승원이는 당근을 좋아해서 당근마킷에 엔지니어로 취업했다. 당근을 매우좋아하기 때문에 차도 당근차를 샀다. 이 당근차는 한칸 움직일 때마다 당근을 내뿜으면서 간다. 즉, "한칸" 움직일 때 "당근한개"가 소모된다는 것이다. 승원이는 오늘도 아침 9시에 일어나 당근마킷으로 출근하고자 한다. 승원이는 최단거리로 당근마킷으로 향한다고 할 때 당근몇개를 소모해야 당근마킷에 갈 수 있는지 알아보자. 이 때 승원이는 육지로만 갈 수 있으며 바다로는 못간다. 맵의 1은 육지며 0은 바다를 가리킨다. 승원이는 상하좌우로만 갈 수 있다.
입력
맵의 세로길이 N과 가로길이 M 이 주어지고 이어서 N * M의 맵이 주어진다. 그 다음 줄에 승원이의 위치(y, x)와 당근마킷의 위치(y, x)가 주어진다.
출력
당근을 몇개 소모해야 하는지 출력하라.
범위
1 <= N <= 100
1 <= M <= 100
예제입력
예제출력
해설
이 문제는 어떤 문제일까요? 바로 "가중치가 같은 그래프 내의 최단거리알고리즘" 문제입니다. 한칸씩 이동할 때마다 당근 한개를 쓰기 때문에 가중치가 같은 그래프이며 여기서 최단거리를 구하는 알고리즘이기 때문이죠. 그렇다면 BFS를 통해 최단거리 배열을 만들어서 해야 합니다.
정답코드
#include<bits/stdc++.h>
using namespace std;
const int max_n = 104;
int dy[4] = {-1, 0, 1, 0};
int dx[4] = {0, 1, 0, -1};
int n, m, a[max_n][max_n], visited[max_n][max_n], y, x, sy, sx, ey, ex;
int main(){
scanf("%d %d", &n, &m);
cin >> sy >> sx;
cin >> ey >> ex;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cin >> a[i][j];
}
}
queue<pair<int, int>> q;
visited[sy][sx] = 1;
q.push({sy, sx});
while(q.size()){
tie(y, x) = q.front(); q.pop();
for(int i = 0; i < 4; i++){
int ny = y + dy[i];
int nx = x + dx[i];
if(ny < 0 || ny >= n || nx < 0 || nx >= m || a[ny][nx] == 0) continue;
if(visited[ny][nx]) continue;
visited[ny][nx] = visited[y][x] + 1;
q.push({ny, nx});
}
}
printf("%d\n", visited[ey - 1][ex - 1]);
// 최단거리 디버깅
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cout << visited[i][j] << ' ';
}
cout << '\n';
}
return 0;
}
상세설명
queue<pair<int, int>> q;
visited[sy][sx] = 1;
q.push({sy, sx});
while(q.size()){
tie(y, x) = q.front(); q.pop();
for(int i = 0; i < 4; i++){
int ny = y + dy[i];
int nx = x + dx[i];
if(ny < 0 || ny >= n || nx < 0 || nx >= m || a[ny][nx] == 0) continue;
if(visited[ny][nx]) continue;
visited[ny][nx] = visited[y][x] + 1;
q.push({ny, nx});
}
}2차원배열이기 때문에 y, x를 담기 위해 pair를 정의하고 visited 배열의 값을 1로 설정한 뒤 시작지점을 큐에 푸시를 합니다. 그 이후 큐의 크기만큼 while 반복문을 돌며 탐색을 진행합니다. 큐의 가장 앞부분에 있는 좌표를 끄집어내어 탐색을 다시 이어가며 4방향을 탐색하며 다시 visited배열을 갱신하며 큐에 넣으며 진행합니다. 자, 제가 최단거리배열을 만드는게 핵심이라고 했죠?
visited[ny][nx] = visited[y][x] + 1;이렇게 내가 가야할 곳인 ny, nx에 지금 있는 곳 y, x 로부터 + 1를 하게 되면 어떻게 될까요?
바로 최단거리 배열은 이렇게 쌓이게 됩니다.
9
1 0 5 0 9
2 3 4 0 8
0 0 5 6 7
0 0 6 7 8
0 0 7 8 9이렇게 최단거리배열을 만들었을 뿐인데 "해당 목표좌표를 출력"하니 그 부분에 해당하는 최단거리값이 출력되는 것을 볼 수 있죠?
DFS와 BFS비교
|
이름
|
설명
|
|
DFS
|
메모리를 덜 씀. 절단점 등 구할 수 있음. 코드가 좀 더 짧으며 완전탐색의 경우에 많이 씀.
|
|
BFS
|
메모리를 더 씀. 가중치가 같은 그래프내에서 최단거리를 구할 수 있음. 코드가 더 김
|
문제에서 "퍼져나간다", "탐색한다" 이 2글자가 있으면 반드시 DFS, BFS가 생각이 나야 합니다. 한쪽은 깊이우선탐색이고 한쪽은 너비우선탐색이라 서로의 길이 다르지만 뭐 어떻습니까. 모두다 퍼져나거나 탐색할 때 쓰이는 알고리즘인 걸요.
트리순회
트리순회라고 하면 이진트리내에서 트리를 순회하는 알고리즘을 의미합니다. 트리를 기준으로 순회하는 4개의 알고리즘이 있습니다.
후위순회
후위순회(postorder traversal)는 자식들 노드를 방문하고 자신의 노드를 방문하는 것을 말합니다.
수도코드
postorder( node )
if (node.visited == false)
postorder( node->left )
postorder( node->right )
node.visited = true
전위순회
전위순회(preorder traversal)는 먼저 자신의 노드를 방문하고 그 다음 노드들을 방문하는 것을 말합니다.
수도코드
preorder( node )
if (node.visited == false)
node.visited = true
preorder( node->left )
preorder( node->right )중위순회
중위순회(inorder traversal)는 왼쪽 노드를 먼저 방문 그다음의 자신의 노드를 방문하고 그 다음 오른쪽 노드를 방문하는 것을 말합니다.
수도코드
inorder( node )
if (node.visited == false)
inorder( node->left )
node.visited = true
inorder( node->right )
레벨순회
레벨순회(level traversal)입니다. 앞서 설명한 BFS를 생각하시면 됩니다.
Q. 아래의 그래프가 주어졌을 때 preorder, inorder, postorder를 구현하라.
수도코드를 보고 코드를 구축하는 연습을 하셔야 합니다. 아래와 같이 그래프가 주어졌을 때 비어진 함수를 채워서 preorder, inorder, postorder를 구현하고 이 때 방문했을 때 해당 노드를 출력하는 것을 구현해보세요.
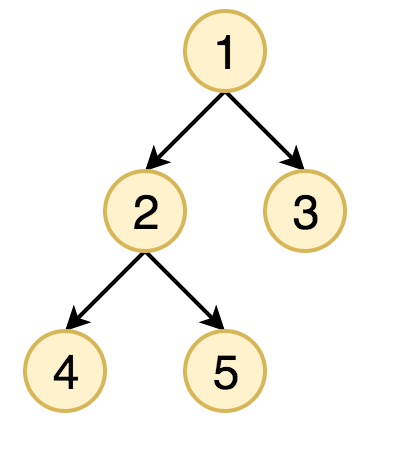
#include <bits/stdc++.h>
using namespace std;
vector<int> adj[1004];
int visited[1004];
void postOrder(int here){
}
void preOrder(int here){
}
void inOrder(int here){
}
int main(){
adj[1].push_back(2);
adj[1].push_back(3);
adj[2].push_back(4);
adj[2].push_back(5);
int root = 1;
cout << "\n 트리순회 : postOrder \n";
postOrder(root); memset(visited, 0, sizeof(visited));
cout << "\n 트리순회 : preOrder \n";
preOrder(root); memset(visited, 0, sizeof(visited));
cout << "\n 트리순회 : inOrder \n";
inOrder(root);
return 0;
}정답코드
#include <bits/stdc++.h>
using namespace std;
vector<int> adj[1004];
int visited[1004];
void postOrder(int here){
if(visited[here] == 0){
if(adj[here].size() == 1)postOrder(adj[here][0]);
if(adj[here].size() == 2){
postOrder(adj[here][0]);
postOrder(adj[here][1]);
}
visited[here] = 1;
cout << here << ' ';
}
}
void preOrder(int here){
if(visited[here] == 0){
visited[here] = 1;
cout << here << ' ';
if(adj[here].size() == 1)preOrder(adj[here][0]);
if(adj[here].size() == 2){
preOrder(adj[here][0]);
preOrder(adj[here][1]);
}
}
}
void inOrder(int here){
if(visited[here] == 0){
if(adj[here].size() == 1){
inOrder(adj[here][0]);
visited[here] = 1;
cout << here << ' ';
}else if(adj[here].size() == 2){
inOrder(adj[here][0]);
visited[here] = 1;
cout << here << ' ';
inOrder(adj[here][1]);
}else{
visited[here] = 1;
cout << here << ' ';
}
}
}
int main(){
adj[1].push_back(2);
adj[1].push_back(3);
adj[2].push_back(4);
adj[2].push_back(5);
int root = 1;
cout << "\n 트리순회 : postOrder \n";
postOrder(root); memset(visited, 0, sizeof(visited));
cout << "\n 트리순회 : preOrder \n";
preOrder(root); memset(visited, 0, sizeof(visited));
cout << "\n 트리순회 : inOrder \n";
inOrder(root);
return 0;
}
/*
트리순회 : postOrder
4 5 2 3 1
트리순회 : preOrder
1 2 4 5 3
트리순회 : inOrder
4 2 5 1 3
*/수도코드처럼 어떤 부분에 출력함수를놓을지만 생각하면 됩니다. 사실 여기서 visited배열은 쓰지 않아도 됩니다. 단방향 간선이기 때문이고 DAG이기 때문입니다. 하지만 수도코드에 있기 때문에 넣어서 구현했습니다.
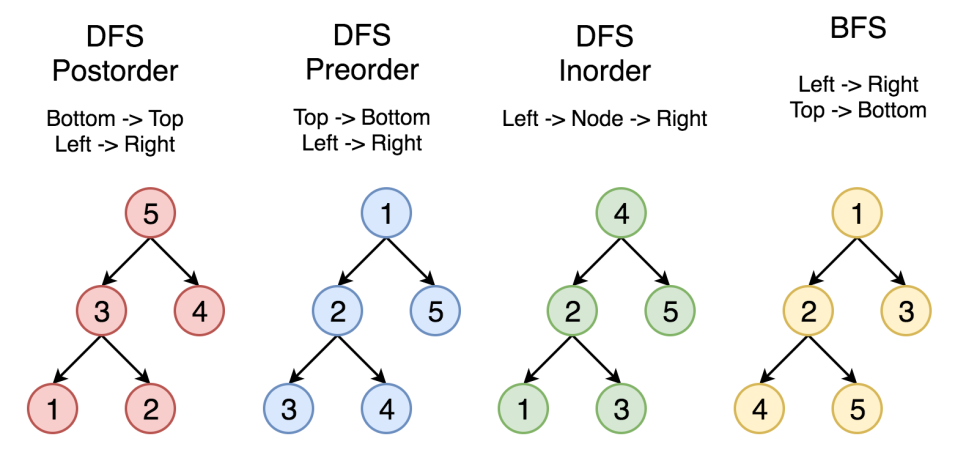
지금 보시면 postorder의 경우 4, 5, 2, 3, 1 이런식으로 방문되는 것을 볼 수있죠? 구현해보시고 위그림과 비교하면서 공부하시면 됩니다.
[출처] [알고리즘 강의] 2주차. 그래프이론, DFS, BFS, 트리순회|작성자 큰돌
'C++ > 알고리즘' 카테고리의 다른 글
| DFS 코드 구현 2가지 방법 (0) | 2022.08.09 |
|---|---|
| <알고리즘> 2차원 배열 회전 (0) | 2022.04.22 |
| <알고리즘> 입출력 싱크 (0) | 2022.04.22 |
| <알고리즘> 2차원 배열 수정하는 함수 (0) | 2022.04.22 |
| <알고리즘> n진법 변환 (0) | 2022.04.22 |